二叉排序树
二叉搜索树(BST)是二叉树的一种特殊表示形式,它满足如下特性:
- 每个节点中的值必须大于(或等于)存储在其左侧子树中的任何值。
- 每个节点中的值必须小于(或等于)存储在其右子树中的任何值。
代码实现:
struct TreeNode {
int val; // 节点的值
TreeNode *left; // 指向左子树的指针
TreeNode *right; // 指向右子树的指针
// 构造函数初始化
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
二叉排序树的搜索操作
循环实现:
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while (root != nullptr) {
if (root->val == val)
return root;
else if (val < root->val)
root = root->left;
else
root = root->right;
}
return nullptr;
}
};
递归实现:
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (!root)
return nullptr;
if (val == root->val)
return root;
else if (val < root->val)
return searchBST(root->left, val);
else
return searchBST(root->right, val);
}
};
二叉排序树的插入操作
循环实现:
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (!root)
return new TreeNode(val);
TreeNode *p = root;
while (p) {
if (val < p->val) {
if (p->left == nullptr) {
p->left = new TreeNode(val);
break;
}
p = p->left;
}
else if (val > p->val){
if (p->right == nullptr) {
p->right = new TreeNode(val);
break;
}
p = p->right;
}
}
return root;
}
};
递归实现:
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (!root)
return new TreeNode(val);
if (val == root->val)
return root;
else if (val < root->val)
root->left = insertIntoBST(root->left, val);
else
root->right = insertIntoBST(root->right, val);
return root;
}
};
二叉排序树的删除操作
代码实现:
class Solution {
public:
// 删除节点的函数,返回更新后的树根
TreeNode* deleteNode(TreeNode* root, int key) {
// 基本情况:如果根节点为空,返回空
if (root == nullptr) {
return nullptr;
}
// 如果 key 比当前节点的值小,递归在左子树中寻找并删除
if (root->val > key) {
root->left = deleteNode(root->left, key);
return root;
}
// 如果 key 比当前节点的值大,递归在右子树中寻找并删除
if (root->val < key) {
root->right = deleteNode(root->right, key);
return root;
}
// 找到要删除的节点
if (root->val == key) {
// 情况1: 节点为叶子节点
if (!root->left && !root->right) {
delete root; // 释放该节点的内存
return nullptr; // 返回空指针,表示该节点已删除
}
// 情况2: 只有左子树
if (!root->right) {
TreeNode* temp = root->left; // 暂存左子树
delete root; // 释放该节点
return temp; // 返回左子树替代该节点
}
// 情况3: 只有右子树
if (!root->left) {
TreeNode* temp = root->right; // 暂存右子树
delete root; // 释放该节点
return temp; // 返回右子树替代该节点
}
// 情况4: 左右子树均不为空
// 找到左子树中的最大节点(即前驱节点)
TreeNode *pre = root, *cur = root->left;
while (cur->right) {
pre = cur; // pre 是 cur 的父节点
cur = cur->right; // cur 一直走到最右边
}
// 用前驱节点的值替换当前节点的值
root->val = cur->val;
// 调整父节点的指针,处理删除前驱节点后的连接
if (pre != root) {
pre->right = cur->left; // 如果前驱节点不是 root 的直接左子节点
} else {
pre->left = cur->left; // 如果前驱节点是 root 的直接左子节点
}
// 释放前驱节点的内存
delete cur;
return root;
}
return root;
}
};
二叉排序树的查找分析
- 与折半查找类似,和给定值比较的关键字的个数不超过树的深度。不同的是,折半查找长度为n的表的判定树是唯一的,而含有n个结点的二叉排序树却不唯一。
- 含有n个结点的二叉排序树的平均查找长度和树的形态有关。当先后插入的关键字有序时,构成的二叉排序树蜕变成单支树。树的深度为n,其平均查找长度为\frac{n+1}{2},与顺序查找相同,这是最差的情况。
- 在随机情况下,二叉排序树的平均查找长度与\log{n}是等数量级的。
平衡二叉树
平衡二叉树的定义
平衡二叉树又称AVL树。它或者是一颗空树,或者是是具有以下性质的二叉树:
- 它的左子树和右子树都是平衡二叉树,且左右子树的深度之差的绝对值不超过1。
二叉树上结点的平衡因子BF 定义:该结点的左子树的深度减去右子树的深度。
平衡二叉树上所有结点的BF的取值范围为\{-1, 0, 1\}。
#define LH +1 // 左高
#define EH 0 // 等高
#define RH -1 // 右高
typedef int ElemType;
typedef struct BSTNode {
ElemType data;
int bf; // 结点的平衡因子
struct BSTNode *lchild, *rchild; // 左、右孩子指针
}BSTNode, *BSTree;
平衡二叉树的平衡处理
左、右旋操作:
void R_Rotate(BSTree &p) {
// 对以p为根的二叉树排序树作右旋处理,处理之后p指向新的树根结点,即旋转之前的左子树的根结点
BSTNode *lc = p->lchild;
p->lchild = lc->rchild;
lc->rchild = p;
p = lc;
}// R_Rotate
void L_Rotate(BSTree &p) {
// 对以p为根的二叉树排序树作左旋处理,处理之后p指向新的树根结点,即旋转之前的左子树的根结点
BSTNode *rc = p->rchild;
p->rchild = rc->lchild;
rc->lchild = p;
p = rc;
}// L_Rotate
左平衡处理:
void LeftBalance(BSTree &T) {
// 对以指针T所指结点为根的二叉树作做平衡处理,处理之后T指向新的根结点
BSTNode *lc = T->lchild;
switch (lc->bf) {
case LH:
T->bf = lc->bf = EH;
R_Rotate(T);
break;
case RH: // LR: 新结点插入在T的左孩子的右子树上,要作双旋处理
BSTNode *rd = lc->rchild; // rd指向T的左孩子的右子树根
switch (rd->bf) {
case LH: T->bf = RH; lc->bf = EH; break;
case EH: T->bf = lc->bf = EH; break;
case RH: T->bf = EH; lc->bf = LH; break;
}// switch (rd->bf)
rd->bf = EH;
L_Rotate(T->lchild);
R_Rotate(T);
}// switch (lc->bf)
}// LeftBalance
平衡树的查找分析
- N_{h}表示深度为h的平衡树中含有的最少结点数。显然,N_{0} = 0,N_{1} = 1,N_{2} = 2,并且N_{h} = N_{h-1} + N_{h-2} + 1。
- 利用归纳法容易证明:当h \ge 0时, N_{h} = F_{h+2} -1 。(F_{h}斐波拉契数列)
- 时间复杂度为O(\log{n})
B-树
B-树的定义
B-树是一种平衡的多路查找树,一颗m阶的B-树,或为空树,或为满足下列特性的m叉树:
- 树中每个结点至多有m颗子树;
- 若根结点不是叶子结点,则至少有两颗子树;
- 除根之外的所有非终端结点至少有 \lceil m/2 \rceil 颗子树;
- 所有非终端结点中包含以下信息数据
- (n, A_{0}, K_{1}, A_{1}, K_{2}, A_{2}, \dots , K_{n}, A_{n})
- 其中:K_{i} (i = 1, \dots, n)为关键字,且K_{i} < K_{i+1} (i = 1, \dots, n);
- A_{i} (i = 0, \dots, n)为指向子树根结点的指针,且指针A_{i-1}所指子树中所有结点的关键字均小于K_{i}(i = 1, \dots, n)
- A_{n}所指子树中所有结点的关键字均大于K_{n}, n(\lceil m/2 \rceil - 1 \le n \le m-1)为关键字的个数或n+1为子树个数
- 所有叶子结点都出现在同一层次上,并且不带信息。(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
#define m 3 // B-树的阶
typedef struct BTNode {
int keynum; // 结点中关键字个数,即结点的大小
struct BTNode *parent; // 指向双亲结点
KeyType key[m+1]; // 关键字向量,0号单元未用
struct BTNode *ptr[m+1]; // 子树指针向量
Record *recptr[m+1]; // 记录指针向量,0号单元未用
}BTNode, *BTree;
typedef struct {
BTNode *pt; // 指向找到的结点
int i; // i..m 在结点中的关键字序号
int tag; // 1:查找成功,0:查找失败
}Result; // B-树的查找结果类型
B-树的查找操作
Result SearchBTree(BTree T, KeyType K) {
// 在 m 阶B-树T上查找关键字K,返回结果(pt, i, tag)。若查找成功,则特征值tag=1,指针pt
// 所指结点中第i个关键字等于K;否则特征值tag=0,等于K的关键字应插入在指针pt所指
// 结点中第i个和第i+1个关键字之间
BTNode *p = T, *q = nullptr;
bool found = false;
int i = 0;
while (p && !found) {
i = Search(p, K); // 在p->key[1..keynum]中查找,
// 使得i:p->key[i] <= k <= p->key[i+1]
if (i > 0 && p->key[i] == K) found = true;
else { q = p; p = p->ptr[i]; }
}
if (found) return {p, i, 1};
else return {q, i, 0};
}// SearchBTree
B-树的查找分析
- 一般情况下的分析类似二叉平衡树进行,先讨论深度为L+1的m阶B-树所具有的最少结点数。根据B-树的定义,第一层至少有1个结点;第二层至少有2个结点;由于除根之外的每个非终端结点至少有\lceil m/2 \rceil颗子树,则第三层至少有2(\lceil m/2 \rceil)个结点;依次类推,第L+1层至少有2(\lceil m/2 \rceil)^{L-1}个结点。而L+1层的结点为叶子结点。
- 若m阶B-树中具有N个关键字,则叶子结点即查找不成功的结点为N+1,由此有:N+1 \ge 2 * (\lceil m/2 \rceil)^{L-1}
- 反之:L \le log_{\lceil m/2 \rceil}( \frac{N+1}{2} ) +1
- 即在含有N个关键字的B-树上进行查找时,从根结点到关键字所在结点的路径上涉及的结点数不超过log_{\lceil m/2 \rceil}( \frac{N+1}{2} ) +1
B-树的插入操作
一般情况下,结点可如下实现分裂:
假设p结点中已有m-1个关键字,当插入一个关键字之后,结点含有信息为:m, A_{0}, K_{1}, A_{1}, \dots , K_{m}, A_{m}且其中
且其中K_{i} < K_{i+1} \ \ \ \ ( 1 \le i < m )
此时可将p结点分裂为p结点和p`结点两个结点,
其中p结点中含有信息为\lceil m/2 \rceil - 1, A_{0}, (K_{1}, A_{1}), \dots , (K_{\lceil m/2 \rceil-1}, A_{\lceil m/2 \rceil-1})
其中p`结点中含有信息为m - \lceil m/2 \rceil, A_{\lceil m/2 \rceil}, (K_{\lceil m/2 \rceil + 1}, A_{\lceil m/2 \rceil + 1}), \dots , (K_{m}, A_{m})
而关键字K_{\lceil m/2 \rceil}和指针p`一起插入到p的双亲结点。
Status InsertBTree(BTree &T, KeyType K, BTree q, int i) {
// 在 m 阶B-树T上结点q的key[i]与key[i+1]之间插入关键字K
// 若引起结点过大,则沿双亲链进行必要的结点分裂调整,使T仍是m 阶B-树
KeyType x = K;
BTNode *ap = nullptr;
bool finished = false;
while (q && !finished) {
Insert(q, i, x, ap); // 将x和ap分别插入到q->key[i+1]和q->ptr[i+1]
if (q->keynum < m) finished = true; // 插入完成
else { // 分裂结点q
int s = std::ceil(m / 2);
split(q, s, ap);
x = q->key[s]; // 将p->key[s+1..m], q->ptr[s..m]和q->recptr[s+1..m]
q = q->parent; // 移入新结点ap
if (q) i = Search(q, x); // 在双亲结点q中查找x的插入位置
}// else
}// while
if (!finished) NewRoot(T, q, x, ap);
return OK;
}// InsertBTree
B-树的删除操作
若在B-树上删除一个关键字,则首先应找到该关键字所在结点,并从中删除值,若该结点为最下层的非终端结点,且其中的关键字数目不少于\lceil m/2 \rceil,则删除完成,否则要进行 合并结点的操作。
删除最下层非终端结点中的关键字的情形:
- 被删除关键字所在结点中的关键字数目不小于\lceil m/2 \rceil则只需从该结点中删去该关键字K_i和相应指针A_i,树的其他部分不变。
- 被删除关键字所在结点中的关键字数目等于\lceil m/2 \rceil - 1,则需要将其兄弟结点中的最小(或最大)的关键字上移至双亲结点中,而将双亲结点中小于(或大于)且紧靠该上移关键字的关键字下移至被删除关键字所在结点中。
- 被删除关键字所在结点和其相邻的兄弟节点中的关键字数目均等于\lceil m/2 \rceil-1。假设该结点有右兄弟,且其右兄弟结点地址由双亲结点中的指针A_i所指,则在删去关键字之后,它所在结点剩余的关键字和指针,加上双亲结点中的关键字K_i一起,合并到A_i所指兄弟结点中(若没有右兄弟,则合并至左兄弟结点中)。
B+树
B+树的定义
B+树应文件系统所需而出的一种B-树的变型树。一颗m阶的B+树和m阶B-树的差异在于:
- 有n颗子树的结点含有n个关键字,树中每个结点至多有m个关键字
- 根结点至少有2个关键字,除根之外的所有非终端结点至少有 \lceil m/2 \rceil 个关键字
- 所有的叶子结点包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接
- 所有非终端结点可以看成是索引部分,结点中仅含有其子树(根结点)中的最大(或最小)关键字
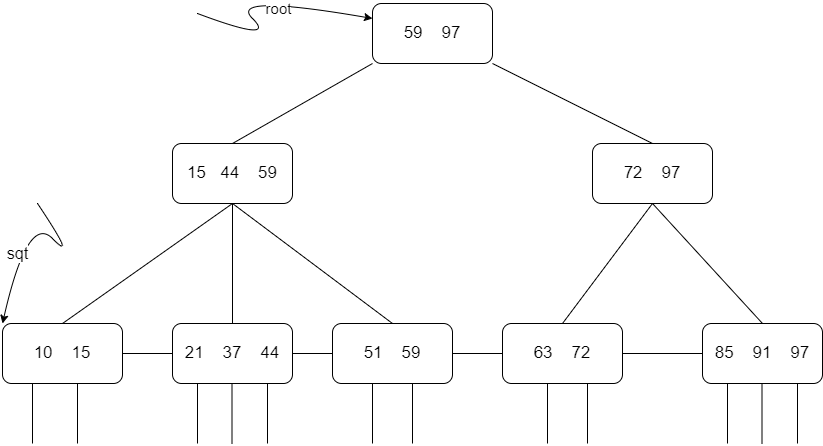
B+树的查找
通常在B+树上有两个指针,一个指向根结点,另一个指向关键字最小的叶子结点。因此,可以对B+树进行两种查找运算:一种是从最小关键字起顺序查找,另一种是从根结点开始,进行随机查找。
注意,在随机查找时,若非终端结点上的关键字等于给定值,并不终止,而是继续向下直到叶子结点。因此,在B+树,每次随机查找都是走了一条从根到叶子结点的路径。
B+树的插入
B+树的插入仅在叶子结点上进行,当结点中的关键字个数大于m时要分裂成两个结点,它们所包含关键字的个数分别为\lceil \frac{m+1}{2} \rceil和\lceil \frac{m+1}{2} \rceil,并且它们的双亲结点中应同时包含这两个结点中的最大关键字。
B+树的删除
B+树的删除也仅在叶子结点上进行,当叶子结点中的最大关键字被删除时,其在非终端结点中的值可以作为一个分界关键字存在。若因删除而使得结点中关键字的个数少于\lceil m/2 \rceil时,其和兄弟结点的合并过程亦和B树类似。
