栈

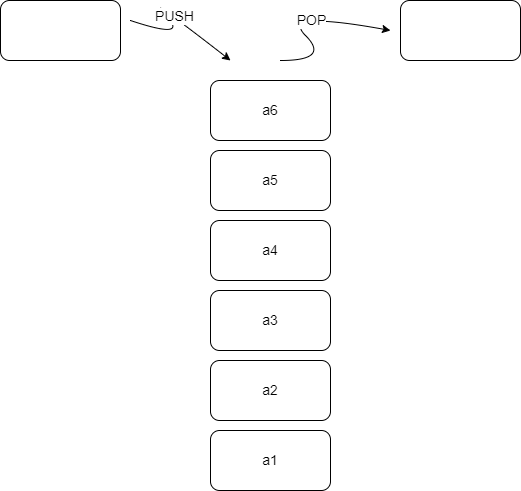
栈，即操作受限的线性表，其特点是仅在表尾进行插入或删除操作。这种特殊的线性表的表尾称为栈顶，表头称为栈底。不含任何元素的空表称为空栈。

栈的修改是遵循后进先出的原则，因此又称为后进先出的线性表（简称LIFO结构）。

栈的数学性质：当有n个不同的元素进栈时，总共有​\frac{2}{n+2} \binom{n}{2n}种可能的出栈序列。

栈的顺序实现

栈的顺序实现遵循如下原则：

• 利用一组地址连续的存储单元以此存放自栈底到栈顶的元素
• 设指针 top指示栈顶元素在栈中的位置，以 top == 0表示空栈
• 一般地，在初始化栈时不应假设栈的最大容量
• 先为栈分配一个基本容量，当栈的空间不够使用时再逐渐扩大
• 设常量 STACK_INIT_SIZE表示存储空间初始分配量，常量 STACK_INCREMENT表示存储分配增量

#define STACK_INIT_SIZE 100   // 栈初始容量
#define STACK_INCREMENT 10    // 栈容量扩展的增量
typedef int SElemType;        // 栈元素的数据类型

// 定义顺序栈结构体
typedef struct {
    SElemType *base;  // 栈底指针
    SElemType *top;   // 栈顶指针
    int stacksize;    // 栈的当前容量
} SqStack;

基本操作的实现

// 初始化栈
void InitStack(SqStack *S) {
    S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType)); // 分配初始空间
    if (!S->base) exit(0);  // 若分配失败，退出
    S->top = S->base;       // 栈顶指向栈底，表示空栈
    S->stacksize = STACK_INIT_SIZE;
}

// 获取栈顶元素
int GetTop(SqStack S, SElemType *e) {
    if (S.top == S.base) return 0;  // 栈空，返回失败
    *e = *(S.top - 1);              // 获取栈顶元素
    return 1;                       // 返回成功
}

// 压栈操作
void Push(SqStack *S, SElemType e) {
    // 判断是否需要扩展栈的空间
    if (S->top - S->base >= S->stacksize) {
        S->base = (SElemType *)realloc(S->base, (S->stacksize + STACK_INCREMENT) * sizeof(SElemType));
        if (!S->base) exit(0);  // 若分配失败，退出
        S->top = S->base + S->stacksize;
        S->stacksize += STACK_INCREMENT;
    }
    *(S->top) = e;   // 将元素压入栈顶
    S->top++;        // 栈顶指针上移
}

// 弹栈操作
int Pop(SqStack *S, SElemType *e) {
    if (S->top == S->base) return 0;  // 栈空，返回失败
    S->top--;                         // 栈顶指针下移
    *e = *(S->top);                   // 将栈顶元素赋值给e
    return 1;                         // 返回成功
}

// 销毁栈
void DestroyStack(SqStack *S) {
    free(S->base);   // 释放栈空间
    S->base = NULL;  // 置空指针
    S->top = NULL;
    S->stacksize = 0;
}

// 判断栈是否为空
int StackEmpty(SqStack S) {
    return S.top == S.base;
}

栈的链式实现

typedef int SElemType;  // 栈元素的数据类型

// 定义栈的节点
typedef struct StackNode {
    SElemType data;            // 栈元素
    struct StackNode *next;    // 指向下一个节点的指针
} StackNode, *LinkStackPtr;

// 定义链栈结构
typedef struct {
    LinkStackPtr top;  // 栈顶指针
    int count;         // 栈中元素的个数
} LinkStack;

基本操作的实现

// 初始化链栈
void InitStack(LinkStack *S) {
    S->top = NULL;   // 初始化栈顶为NULL，表示空栈
    S->count = 0;    // 初始化元素个数为0
}

// 压栈操作
void Push(LinkStack *S, SElemType e) {
    LinkStackPtr newNode = (LinkStackPtr)malloc(sizeof(StackNode));  // 分配新节点
    if (!newNode) exit(0);  // 分配失败，退出
    newNode->data = e;      // 将元素赋值给新节点
    newNode->next = S->top; // 将新节点的next指向当前栈顶节点
    S->top = newNode;       // 更新栈顶指针
    S->count++;             // 栈元素个数加1
}

// 弹栈操作
int Pop(LinkStack *S, SElemType *e) {
    if (S->top == NULL) return 0;  // 栈空，返回失败
    LinkStackPtr temp = S->top;    // 暂存栈顶节点
    *e = temp->data;               // 获取栈顶元素
    S->top = temp->next;           // 将栈顶指针指向下一个节点
    free(temp);                    // 释放原栈顶节点
    S->count--;                    // 栈元素个数减1
    return 1;                      // 返回成功
}

// 获取栈顶元素
int GetTop(LinkStack S, SElemType *e) {
    if (S.top == NULL) return 0;  // 栈空，返回失败
    *e = S.top->data;             // 获取栈顶元素
    return 1;                     // 返回成功
}

// 销毁栈
void DestroyStack(LinkStack *S) {
    while (S->top) {
        LinkStackPtr temp = S->top;
        S->top = S->top->next;
        free(temp);
    }
    S->count = 0;
}

// 判断栈是否为空
int StackEmpty(LinkStack S) {
    return S.top == NULL;
}

共享栈

可用栈底位置相对不变的特性，可以让两个顺序栈共享一个一维顺序表，将两个栈的栈底分别设置在顺序表的表头和表尾。可以更有效地利用存储空间。

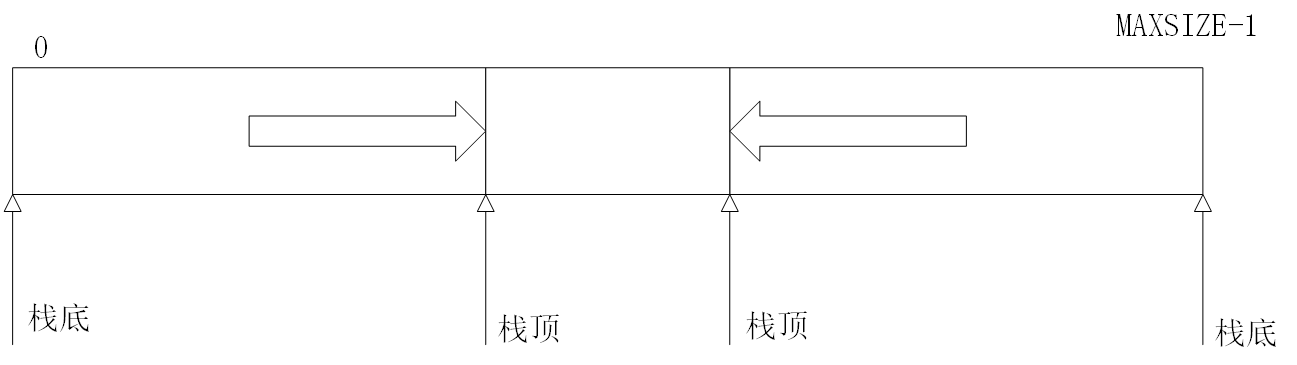
• 判断栈满：top0 - top1 = 1
• 判断空栈：top0 == 1 or top1 == MAXSIZE-1

栈的应用

数制转换

十进制数N和其他d进制数的转换：​N = (N \ \ div \ \ d)*d + N \ \ mod \ \ d

// 进制转换函数
void conversion(int n, int d) {
    LinkStack s;
    SElemType e;
  
    InitStack(&s);
  
    // 将n转换为d进制并压入栈中
    while (n) {
        Push(&s, n % d);
        n /= d;
    }
  
    // 输出栈中保存的每一位数，栈的作用是逆序输出
    while (!StackEmpty(s)) {
        Pop(&s, &e);
        printf("%d", e);  // 打印出栈元素
    }
    printf("\n");
}

表达式求值

队列

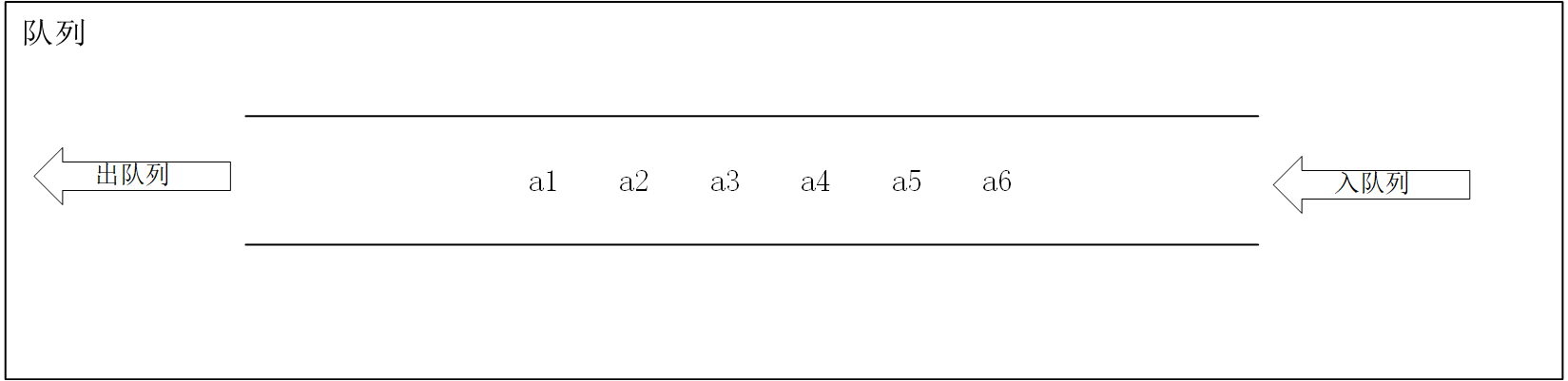
队列，也是操作受限的线性表，其特点是只允许在表的一端进行插入，而在另一端进行删除元素。在队列中，允许插入的一端称为队尾 rear，允许删除的一端称为表头 front。

队列的修改是遵循先进先出的原则，因此又称为先进先出的线性表（简称FIFO结构）。

队列的顺序实现

顺序队列

队列的顺序实现是指分配一块连续的存储空间存放队列元素，并附设两个指针：队头指针 front和队尾指针 rear。

• 队空：Q.front = Q.rear = 0
• 出队操作：队不为空时，Q.front = Q.front + 1
• 入队操作：队未满时，Q.rear = Q.rear + 1

#define MAXSIZE 50  // 定义队列最大长度
typedef int QElemType;  // 定义队列元素类型

// 循环队列结构体
typedef struct {
    QElemType data[MAXSIZE];  // 存储队列元素的数组
    int front;  // 队首指针
    int rear;   // 队尾指针
} SqQueue;

循环队列

把存储队列元素的表从逻辑上视为一个环，称为循环队列。

• 队空：Q.front == Q.rear
• 队满：(Q.rear + 1) % MAXSIZE == Q.font
• 出队操作：Q.front = (Q.front + 1) % MAXSIZE
• 入队操作：Q.rear = (Q.rear + 1) % MAXSIZE
• 队列长度：(Q.rear - Q.front + MAXSIZE) % MAXSIZE

这种实现牺牲了一个存储单元来区分队空和队满，约定以“队头指针在队尾指针的下一位置作为队满的标志”。

#define MAXSIZE 50  // 定义队列最大长度
typedef int QElemType;  // 定义队列元素类型

// 循环队列结构体
typedef struct {
    QElemType data[MAXSIZE];  // 存储队列元素的数组
    int front;  // 队首指针
    int rear;   // 队尾指针
} CircularQueue;

// 初始化队列
void InitQueue(CircularQueue *Q) {
    Q->front = 0;  // 初始化队首指针
    Q->rear = 0;   // 初始化队尾指针
}

// 判断队列是否为空
int QueueEmpty(CircularQueue Q) {
    return Q.front == Q.rear;
}

// 判断队列是否满
int QueueFull(CircularQueue Q) {
    return (Q.rear + 1) % MAXSIZE == Q.front;
}

// 入队操作
int EnQueue(CircularQueue *Q, QElemType e) {
    if (QueueFull(*Q)) {
        printf("队列已满，无法入队！\n");
        return 0;  // 队满则返回失败
    }
    Q->data[Q->rear] = e;  // 将元素放入队尾
    Q->rear = (Q->rear + 1) % MAXSIZE;  // 队尾指针向后移动
    return 1;  // 入队成功
}

// 出队操作
int DeQueue(CircularQueue *Q, QElemType *e) {
    if (QueueEmpty(*Q)) {
        printf("队列为空，无法出队！\n");
        return 0;  // 队空则返回失败
    }
    *e = Q->data[Q->front];  // 获取队首元素
    Q->front = (Q->front + 1) % MAXSIZE;  // 队首指针向后移动
    return 1;  // 出队成功
}

// 获取队列长度
int QueueLength(CircularQueue Q) {
    return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

队列的链式实现